「随机算法专题」距离与相似度的度量

Hamming 空间最近邻（近似）：设有$n$个$d$维的 Hamming 空间上的点，要求给定$q\in\mathbb{H}^d$，在$O(n^{\frac{1}{1 + \varepsilon}})$
时间内找到$(1 + \varepsilon)$-近邻。预处理时间限制为$O(n(d + n^{\frac{1}{1 + \varepsilon}}))$。

要解决这个问题，我们首先需要需要引入一些估计方法。

Min Hash

集合相似度度量：如何判断两个集合$A, B \in [n]$的相似度？

朴素想法：我们可以$O(|A| + |B|)$一一比对其中的元素。

考虑定义集合的相似度：$J(A, B) = \frac{|A \cap B|}{|A \cup B|}$。特别地，$J(\varnothing, \varnothing) = 0$。

假设存在一个随机哈希$h$，能够将$[n]$中的元素均匀随机映射到某个域上。那么$A$和$B$中的元素可以近似看作在$[n]$中均匀随机生成的数。

设$h_{\min}(S) = \min_{x \in S} h(x)$。由于随机哈希，$h(x) = h_{\min}(S)$的概率是$\frac{1}{|S|}$。也就是说重复若干次随机哈希的过程，我们可以让每个数的哈希值成为最小值的次数差不多一致。这启发我们在判断集合中是否存在某个相同元素时，可以通过随机哈希转化为比较最小值的问题。

引理：$\text{Pr}[h_{\min}(A)=h_{\min}(B)] = J(A, B)$。如果两者相等，说明此次哈希随机到的数在两边都出现了。否则必然只在一边出现。

Chernoff bound: 设$x_1, \ldots, x_T$是$\{0, 1\}$上的独立随机变量，$\bar{x}$为其均值，$\mu = E[\bar{x}]$。则对$t\in[0, 1]$有

$$\text{Pr}\left[ \left| \bar{X} - \mu \right| \ge t \mu \right] \le 2e^{-t^2T\mu/3}$$

使用上述不等式可以分析需要的哈希个数，但要注意这和答案本身是有直接的关系的。

Sim Hash

向量的相似性度量：判断高维空间两个向量的相似度？

相似度的定义：$\sigma(\vec x, \vec y) = \frac{(\vec x, \vec y)}{||\vec x||_2, ||\vec y||_2}$，即$\cos\theta(\vec x, \vec y)$。范数：$||\vec{x}||_p = (\sum x_i^p)^{\frac1p}$。

类似 Min Hash，我们希望通过概率反映$\sigma(\vec x, \vec y)$。这样就可以通过多次重复随机来近似计算相似度。

考虑生成$d$维空间的一个随机高斯向量$\vec w$（先每一维分别独立服从正太分布，然后单位化）。定义

$$h(x) =\begin{cases} 1 & (\vec w, \vec x)\ge 0\\ 0 & \text{Otherwise} \end{cases}$$

那么我们声称：$\text{Pr}[h(x)\ne h(y)] = \frac{\theta(\vec x, \vec y)}{\pi}$。下图是二维的情况：

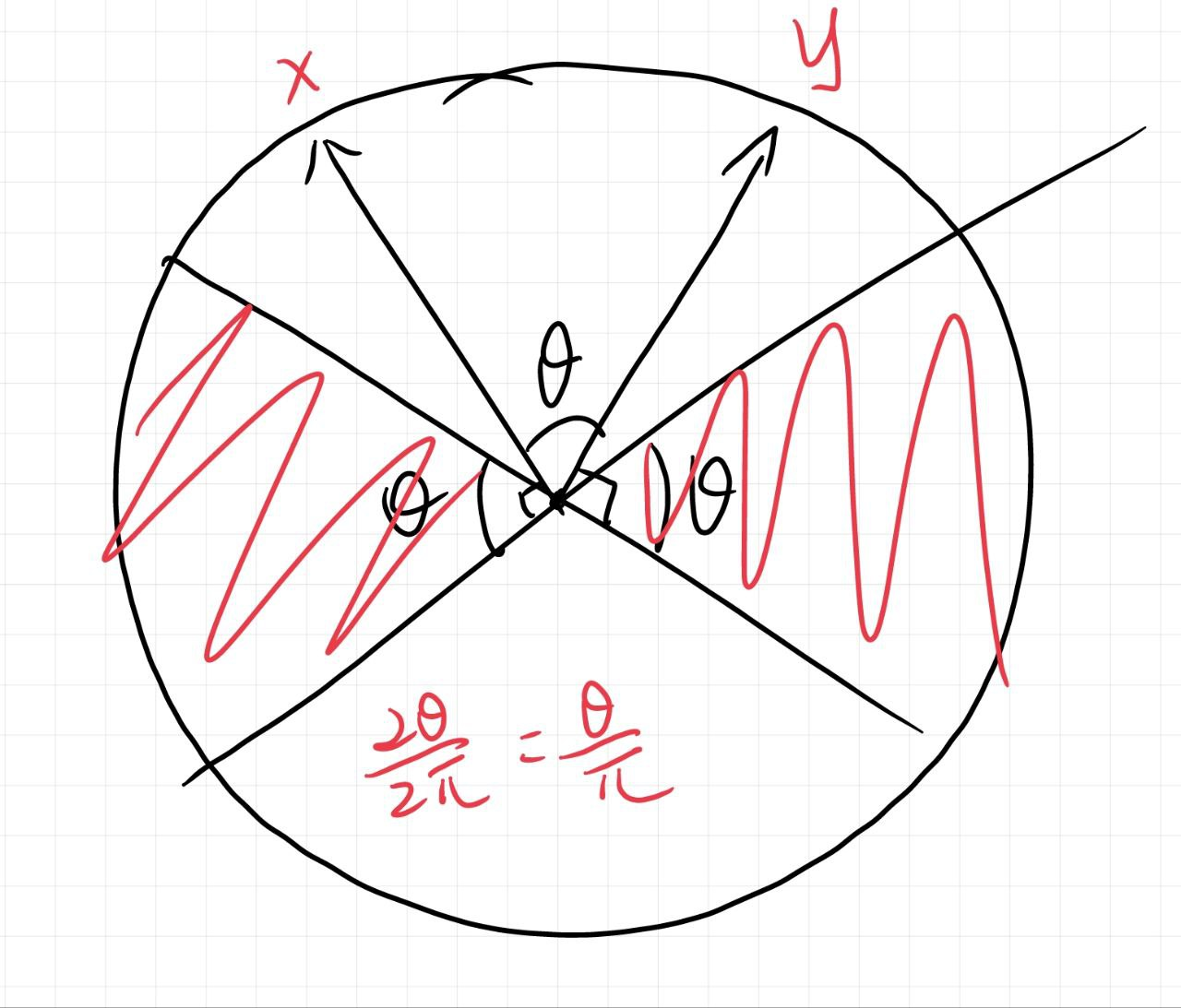
取$T$个独立随机哈希，重复计算即可逼近相似度。

这时如果令$f(\vec x) = [h^{(1)}(\vec x), h^{(2)}(\vec x), \ldots, h^{(T)}(\vec x)]$，就会发现$\sigma(\vec x, \vec y)\approx \frac{1}{T} \text{popcount}(f(\vec x)\oplus f(\vec y))$。

因此可以将$f$视作$\mathbb{R}^d$到$T$维 Hamming 空间（超立方体空间）的映射。

于是我们就得到了$T$维 Hamming 空间中距离的一个估计函数：$\text{dist}_H(f(\vec x), f(\vec y)) \approx \frac{T\theta(\vec x, \vec y)}{\pi}$。

Hamming 空间近似最近邻

注意到 Sim Hash 中给出的估计函数是关于$f(\vec x)$和$f(\vec y)$的距离。如果要直接估计$p, q\in \mathbb{H}^d$的距离的话，就需要找到某个映射$f: \mathbb{H}^d \to \mathbb{H}^d$，使得$\text{dist}_H(f(p), f(q)) = \text{dist}_H(p, q)$。

不难想到取$f$为随机$d$阶排列。生成随机排列：$a_i$和前面随机一个数交换。

当然这道题要求找到$(n + \varepsilon)$-近邻，因此对于询问的$q$我们要找到距离最小的点。

其实结合刚刚的 Min Hash，如果将 Hamming 空间中的点视作$[d]$的子集，那么$f$就相当于是一个随机哈希。而如果取了足够多的$f$，那么$q$与$q$的近似最近邻的相同部分总会在某个哈希中被 roll 到前几个位置上去。基于这样的思想，我们可以用 LCP 来去掉不优的点。

假设取了$N$个$f$。

考虑所有$\{ \text{LCP}(f^{(i)}(p), f^{(i)}(q)) \}_{p\in S,1\le i\le N}$。我们找到其中长度最大的$2N$个$LCP$对应的$p$，然后计算这些点与$q$的最近邻。

参数分析略（太复杂了没学会）。