做题总结

构造题

Atcoder5093

题面

考虑增量。对于一个大小为 k 的图，我们加一个点进去。那么我们求出原本这个图的哈密尔顿回路的最大值 M，则我们新连的边只要大于 M，就不会和以前的路径冲突。现在我们考虑新连的路径互不冲突。考虑构造一个序列$a=\left\langle 1,2,4,7,12,20,29,38,52,73 \right\rangle$这个序列满足所有的$a_i$和$a_i+a_j$是互不相同的。因此我们第 k+1 个点连向第 i 个点的边权设为$(M+1)\times a_i$。这样就行了。

代码

AtCoder 5167

题面

考虑分治，每次把当前点集分成两个点集，连二分图，然后左右递归做。

由于左右两边点集不相交，因此两边递归下去连出来的二分图也是不相交的。

level 就是当前递归的层数。

标算是一个鬼畜的 lowbit 构造法，不太可扩展。

代码

字符串

CF 427D

题面

一个串建 SAM，另一个串在上面跑就行了。跑的时候要记一下另一个串的当前长度和状态数。

代码

CF 316G3

题面

把所有串（包括第一个串）连起来，加一个分隔符（{）建一个 SAM，统计状态数的时候分串统计。然后统计每个状态的贡献就行。

代码

CF 204E

题面

建一个广义 SAM，然后用 Map 统计一下各个串是否经过这个状态以及经过次数，统计的时候和状态数乘一乘就行。

代码

ZJOI2015 诸神眷顾的幻想乡

题面

最多只有 20 个叶结点，所以以每个叶结点为根分别建 Trie，然后合并成一个 Trie，然后在 Trie 上 BFS，每次从父节点的 Last 扩展为当前的结点建 SAM。然后统计本质不同状态数就行。

代码

数据结构

ZR 1037C

题面

长度相同的一起处理，本质不同的长度是根号级别的。复杂度$O(\sqrt{n})$。

CF 438D

题面

线段树，均摊

代码

UOJ 228

题面

对于区间$\max-\min\le 1$的情况开根，有两种情况：

1. 开根后差仍为 1，相当于一个区间减；
2. 开根后变成相同的数，相当于区间覆盖；

对于这两个标记，在区间覆盖的时候清空区间加的标记；在下传的时候先覆盖再加。均摊$O(n\log_2n\log_2\log_2n)$。

代码

LOJ 121

每条边存在的时间是一个区间，那么我们按时间建线段树，然后每个区间被分成 log 个标记。于是我们在线段树上 DFS，使用可撤消并查集维护连通性即可。

代码

BZOJ1568 JSOI2008

李超线段树，标记永久化一下，即查询的时候查询路径上的标记。
复杂度$O(n\log_2n)$。

代码

BZOJ2038

典型的莫队。注意 Luogu 的数据可能区间长度为 1。在提交的时候要删调试的文件（吃一发 WA）

代码

CF1221F

显然可以把所有点都放到$y=x$上方，这样转化之后有$\forall(x,y),x<y$。

考虑将所有点按照纵坐标从小到大排序。则我们做一个横着向上的扫描线，每次加入一些点后，我们相当于要合理画出一条竖线，使得横线，竖线，$y=x$围成的三角形内的点权和减掉三角形直角边边长最大。这本质就是线段树上最大右边缘区间和，可以直接维护。在扫描线向上延伸的时候要在对应结点减去前后位置的差，这样就可以顺便减掉边长（可以理解为边长差分）。

离散化一下，显然正确性不会变。

代码

ZJOI2019 线段树

题面较长。

容易想到，转化为概率问题。每次我们的操作有$\frac{1}{2}$的可能被执行。不妨设$f(u)$表示线段树的结点$u$的 tag 值为 1 的概率。那么我们执行一次操作，结点的$f(u)$会怎么变化？

我们将一次操作中的结点分类：

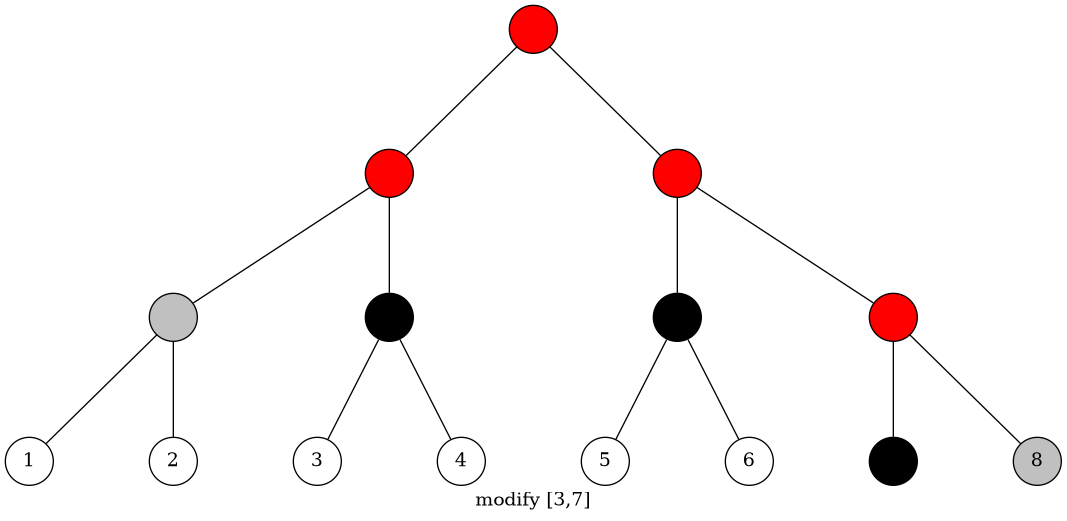
黑点代表被完全覆盖，红点表示被部分覆盖，灰点表示它有可能接受父节点的 pushdown。

若进行一次操作：

1. 黑点的$f(u)$是$1$；
2. 红点的$f(u)$是$0$；
3. 灰点的$f(u)$，取决于其祖先的点上是否有 tag。

因此光定义$f(u)$并不能很好地处理灰点的情况。我们还定义$g(u)$表示，$u$及其祖先中出现 tag 值为 1 的概率。

对于$g(u)$，若进行一次操作：

1. 黑点的$g(u)$为$1$（它自己有 tag）；黑点的儿子（子树）的$g(u)$也是$1$；
2. 红点的$g(u)$为$0$；
3. 灰点的$f(u)$为$g(u)$，而$g(u)$则不变。

因此我们得到了转移的式子：

1. 黑点：$f(u)=\frac{1}{2}(f(u)+1)$，$g(v)=\frac{1}{2}(g(v)+1)(v\in T_u)$；
2. 红点：$f(u)=\frac{1}{2}f(u)$，$g(u)=\frac{1}{2}g(u)$；
3. 灰点：$f(u)=\frac{1}{2}(f(u)+g(u))$。

使用线段树维护即可。

时间复杂度$O(n\log_2n)$。

代码

子异和

设$f(S)=\bigoplus_{x\in S}x$，设$F(S)=\sum_{T\subseteq S} f(T)$。

给出一棵$n$个点带点权树。要求支持$m$次操作：

• 路径的权值都异或$x$；
• 求路径的权值集合的$F$值。

$n,m\le 2\times 10^5,a_i\le 10^9$。

位运算 按位考虑 线段树 树链剖分

首先考虑$F$怎么算。先按位考虑。那么问题转化为 01 集合的$F$值。设该集合有$x$个$0$，$y$个$1$。那么可以得到$F(S)=2^{x+y-1}[y>0]$。于是我们发现这只和集合大小有关。

考虑树上的问题，那么我们的问题就转化为 01 点权树的操作。然而树链剖分维护的复杂度是$O(n\log_2^2n)$的，再加上按位考虑就是$O(n\log_2^3n)$的。

不妨把所有位合在一起考虑。因为我们只需要查询当前路径的第$k$位上是否有 1。那么也就是查询路路径 or。要支持路径 or，路径 xor，我们可以维护$a_u,b_u,c_u$分别表示当前区间的数哪些位都是 1，哪些位都是 0，哪些位是 01 都出现了的。那么在区间异或的时候对$a_u,b_u$做一些位运算即可。在向上合并信息的时候可以用$a,b$更新$c$。

总时间复杂度$O(n\log_2^2n)$。

代码

图论

AtCoder 5168

题面

每行，每列建点，那么在 (x,y) 放一个权值为 w 的卡相当于连一条 (x,y,w) 的边。我们选的方案则一定是一个基环树森林。基环树点数等于边数，则每一条边可以不重不漏地选择一个端点，相当于在这一行（列）被选。于是像找 MST 一样贪心找最大权基环树森林就行。

代码

BZOJ1001 狼抓兔子

最小割的题，Get 到了一个给无向边建流的 Trick。似乎更好的做法是平面图最小割转对偶图最短路，但我懒所以直接 Dinic 过了。

代码

ZR 308

动态加点求桥。

可以离线并查集维护。首先读下来所有边并建出一个桥的生成树（即加入并查集的边构成的树）。然后再扫一遍边集，如果遇到桥就加 1，否则就删除两点路径上的边的桥标记。使用并查集树上的合并技巧即可。

时间复杂度$O(n\log_2n)$。

代码

CF1243 0-1MST

求的是 0 连通块的个数。每次加入一个点，看这个点可以和当前的哪些连通块合并，于是遍历所有与这个点有关的边，统计到每个连通块的边数，就可以判断是否存在 0 的边。

时间复杂度$O(n\log_2n+m)$。$O(n\log_2n)$是并查集。

计数

AtCoder 5169

题面

一个计数题。首先我们要知道，给 n 个人分不超过 r 个球的方案数是$\dbinom{n+r}{r}$的。相当于给$n+1$个人分 r 个球，第$n+1$个人是一个工具人。

题意要求从大到小排序后$a_m=a_{m+1}$，则我们转化为求$a_m>a_{m+1}$的方案数，然后用总方案数减。

我们枚举$x$，则转化为求出$a_m=x,a_{m+1} \le x-1,\sum_{i=1}^na_i\le S$，的方案数。用差分的方法转化为求$a_m\ge x,a_{m+1}\le x-1,\sum_{i=1}^na_i\le S$的方案数。然后对$a_{m+1\sim n}\le x-1$容斥一下，这样相当于球的上限是$S-mx-ix$，i 是枚举的$a_k>x$的个数。

代码

CF1221G

定义$f(S)$表示边权属于集合$S$的方案数。这样容斥一下：

$$Ans=f(0,1,2)-f(0,1)-f(1,2)-f(0,2)+f(0)+f(1)+f(2)-f(\varnothing)$$

接下来挨个分析：

1. 显然，$f(0,1,2)=2^n$。
2. $f(0,2)$相当于每个连通块染一种颜色，则设连通块数量为$C$，那么$f(0,2)=2^C$。
3. $f(0)$相当于每个点权值为 0，但孤立点则权值任意。设孤立点个数为$I$，则$f(0)=2^I$。
4. $f(2)=f(0)$。
5. $f(1)$即二分图染色。如果存在非二分图连通块则$f(1)=0$；否则$f(1)=2^C$。
6. $f(\varnothing)$与边数有关，如果边数为 0 则$f(\varnothing)=2^n$，否则$f(\varnothing)=0$。
7. $f(1,2)=f(0,1)$。

最后考虑$f(0,1)$，它相当于是图的独立集个数。则设$f(S)$表示 G 的导出子图$G[S]$的独立集数。那么显然可以枚举当前点是否属于独立集来计数。而合法的状态数不多。采用记忆化搜索，事实上最多枚举$2^{\frac{n}{2}}$次，然后剩下的就根据记忆化的结果直接返回，复杂度是$O(2^{\frac{n}{2}})$的。

总复杂度$O(2^{\frac{n}{2}})$。

代码

LG4980

Polya 模板题

$$Ans=\frac{1}{n}\sum_{i=1}^nn^{\gcd(n,i)}\\ =\frac{1}{n}\sum_{d|n}n^d\varphi\left(\frac{n}{d}\right)$$

代码

BZOJ1002 轮状病毒

正解是基尔霍夫矩阵树定理，但递推式很简单，$f_i=3f_{i-1}-f_{i-2}+2$。

高精度即可。

代码

BZOJ3202 SDOI2013 项链

题解 1

题解 2

总结一下这题的细节与技巧：

1. 不能费马小定理求逆元，因为模数有时不是质数。
2. LL 乘快速幂的时候要先取模，不然可能溢出。
3. 注意掌握莫比乌斯反演与容斥的小技巧。

代码

BZOJ1547 周末晚会

通过 Burnside 定理转化为求 01 链的相邻 1 个数不超过 k 的方案数，并且要求首尾的 1 连起来个数不超过 k。

如果$n\le k$那么可以随便染。如果$n>k,d\le k$则环数不超过$k$，只要不全染 1 就没事。否则考虑 DP。

$f[i,j]$表示 i 个数末位 k 个为 1 的方案数（不考虑首位和的情况）。最后减掉不合法的方案即可。

代码

ZR996 空

具体就看题解了。记两个 Trick。

首先是字符串子序列匹配方案数和具体的字符是没有关系的，因此枚举最后一段的长度可以转化为组合计数问题。

然后就是组合数化简的技巧：对于$f(n,k)=\sum_{i=0}^n\binom{i+k}{k}p^i$，可以写成递推的形式：

$$\begin{aligned} f(n,k)&=\sum_{i=0}^n\binom{i+k-1}{k-1}p^i+\sum_{i=0}^n\binom{i+k-1}{k}p^i\\ &=f(n,k-1)+\sum_{i=0}^n\binom{i+k-1}{i-1}p^i\\ &=f(n,k-1)+\sum_{i=0}^{n-1}\binom{i+k}{i}p^{i+1}\\ &=f(n,k-1)+p\sum_{i=0}^{n}\binom{i+k}{i}p^i-\binom{n+k}{n}p^{n+1}\\ &=f(n,k-1)+p\cdot f(n,k)-\binom{n+k}{n}p^{n+1} \end{aligned}$$

于是移项得到

$$f(n,k)=\frac{f(n,k-1)-\binom{n+k}{k}p^{n+1}}{1-p}$$

Exercise

定义一个置换$P$的幂周期为最小$k$使得$P^k=I$。

求长度为$n$的所有置换的幂周期乘积$\bmod M$。

$1\le n\le 7500$。

min-max 容斥 DP 组合数学

容易发现，幂周期是环长的 LCM。由于求的是乘积，不妨对每个质因子$p$考虑指数的和。因此我们要求的就是所有幂周期中$p$的指数的和$\bmod (M-1)$。

设$E(p,x)$表示$p$在$x$中的指数。

假设环长是$l_1,l_2,\cdots,l_m$。那么$p$的指数就是$\max E(p,l_i)$。

$$\begin{aligned} \sum_{l}\max_{i=1}^m E(p,l_i) &=\sum_{l}\sum_{\varnothing\subset S\subseteq [m]} (-1)^{|S|-1} \min_{i\in S}E(p,l_i)\\ &=\sum_{l}\sum_{\varnothing\subset S\subseteq [m]} (-1)^{|S|-1}\sum_{x\ge 1}\prod_{i\in S}[E(p,l_i)\ge x] \\ \end{aligned}$$

不妨设

$$f(x,p)=\sum_{l}\sum_{\varnothing\subset S\subseteq [m]} (-1)^{|S|-1}\prod_{i\in S}[E(p,l_i)\ge x]$$

则原式化为$\sum_{x\ge 1}f(x,p)$。

考虑如何计算$f(x,p)$。容易发现，它相当于强制要求子集里的环长都是$p^x$的倍数。考虑 DP。设$s=p^x$，设$g_i$表示$is$个数的贡献和。那么枚举第一个数所在环的长度，得到

$$g_i=-\sum_{j= 1}^i(sj-1)!\binom{si-1}{sj-1}g_{i-j}$$

前面的负号是容斥系数。那么$f(x,p)$就相当于$n$个数中选择$si$个数（剩下的$n-si$个数随便排），然后统计这$si$个数的贡献：

$$f(x,p)=f'(s)=\sum_{i= 1}^{\lfloor\frac{n}{s}\rfloor} \binom{n}{si}(n-si)!g_i$$

那么计算$f(x,p)$的复杂度就是$O(\frac{n^2}{s^2})$。则总复杂度就是$O(\sum_{i=1}^n\frac{n^2}{i^2})=O(\frac{n^2\pi^2}{6})$，能过。

注意，枚举的时候只枚举$p^x$，不要枚举非质因子幂的合数。

代码

博弈

CF1221E

一道不平等博弈的题。由于 a>b，我们考虑 Bob 先手的情况，对于一段连续的.的长度有 4 种情况：

1. $x<b$；
2. $b\le x<a$；
3. $a\le x<2b$；
4. $x\ge 2b$。

如果存在第 2 种情况，那么 Bob 必胜。因为 Alice 能走的 Bob 一定能走，而 Bob 能走的 Alice 不一定能走。

如果存在第 4 种局面，那么 Bob 可以走一发构造出 2，这样他也赢了。

第一种局面没用。第三种局面对于 Alice 和 Bob 都是一次性的。

因此再来考虑 Alice 先手，如果存在 2 那么他就输了；如果存在 2 个及以上的 4 那他也输了。否则可以枚举他走了一步之后的局面，根据局面 3 个数的奇偶性判胜负。

代码

期望

ABC144 F

注意到这是一个拓扑序为 1 到 n 的 DAG，因此我们可以按拓扑序逆序计算每个点到$n$的期望，记为$E(i)$。

$$E(i)=\frac{1}{deg_i}\sum_{(i,j)\in E}E(j)+1$$

现在要求我们删掉一条边，则一个直观的想法是我们计算到达点$i$的概率$P(i)$：

$$P(i)=\sum_{(j,i)\in E}\frac{1}{deg_j}P(j)$$

假设我们删掉了$(i,x)$这条边，则$i$这个点的期望就变成了

$$E'(i)=\frac{1}{deg_i-1}\sum_{(i,j)\in E,(i,j)\ne (i,x)}E(j)+1$$

于是删掉这条边，期望就变成了$E(1)-P(i)(E(i)-E'(i))$。这样就枚举删边更新答案，做完了。

离线

HNOI2016 网格

如果所有路径都包括这个点，那么他们的路径交也包括这个点。因此权值线段树上维护路径交，查询的时候在线段树上二分。要先离散化一下变成不同的权值方便删除。

路径交：边的路径交可以直接取两两 LCA 中最深的两个。点的路径交需要先判是否相交再这么做。

代码

贪心

CF893 D

一个显然的贪心是，只在$a_i=0$的时候充钱。这样不会变劣。

先检查一下最低限度的充钱会不会爆$d$。如果不会爆$d$就在每次$a_i=0$且钱为负数的时候直接充满到$d$。如果在某个时刻钱数大于$d$，就说明之前有一次充多了，直接把钱数变成$d$即可。因为我们检查了最低限度充钱是有解的，因此正确性保证。

复杂度$O(n)$。

数论 / 数学

ZR1090 A+B Problem

算法一：注意到

$$f(n)=\sum_{i=0}^na^ib^{n-i}=\frac{a^{n+1}-b^{n+1}}{a-b}$$

于是直接计算分子，对$(a-b)p$取模，然后除掉$a-b$即可。然而 int128 的精度过不去；

算法二：注意到$f(2x+1)=(a^{x+1}+b^{x+1})f(x), f(2x)=(a^x+b^x)f(x)-a^xb^x$。于是类似快速幂地做就行。复杂度$O(\log_2n)$。

CF1255 E2

设$s_i=\sum_{j=1}^i a_i$。那么原操作可以转化为，将$s_i$加一或减一。这样就是只针对一个数的操作了。

由于$s_i$是单增的，因此对于一个固定的$k$，要把所有$s_i$变成$k$的倍数，我们贪心地把$s_i$变成离它最近的$k$的倍数即可。容易证明这是合法的。代价就是$\sum\min(s_i\bmod k,k-s_i\bmod k)$。

至于$k$，我们只需要选择$s_n$的质因子作为$k$即可。容易证明$k$的约数一定不比$k$劣。这样复杂度为$O(n\log_2n)$。