2021 省选三轮跟训日志 1
文章目录
所谓跟训日志,就是说我是不打省选第三轮的(因为四川没有第三轮)。
矩阵
有一个的矩阵,初始时为全。每次你可以选一个行的子集和列的子集,把所有()变成。
要求在不超过次操作内让()是,其他全部变成。
输出步骤。
。
二进制划分 分治
这题的部分分可以分治,每次将左下和右上的矩阵干掉,这样就变成了两个互不相关的子问题,可以同步解决。
先考虑一个相关的问题 A:
让的是,其他都变成。也就是说我们要选中所有的二元组。
考虑按位划分。对于行号和列号(即)枚举二进制下第位,将第位为的放入集合,其他的放入集合。那么我们让做一次操作,再让做一次操作。这样的操作次数是的。容易证明它可以选中所有的二元组。
那么回到原问题。我们能否将原问题转化为上述问题?
考虑将列(或者行)奇偶分组。这时你会发现原问题被分解为了两个规模是的问题 A。不过这两个不一定能同步做,因此操作次数上界是的。还是太多。
我们考虑做一个优化,使得只需要这一次操作,不需要。
容易发现行号和列号不一定是,只需要保证互不相同,且对角线上的元素的行号和列号相同即可。
那么我们找一组数,使得其中的任意两个数满足:
- 存在使得的二进制第位为,的二进制第位为;
- 存在使得的二进制第位为,的二进制第位为。
这样就意味着,当我们枚举到时,会被选中,当枚举到时,会被选中。因此就不需要这一步操作了。
不妨考虑所有位,有个的二进制数。由于,可以胜任。将这些数作为行号和列号,可以在次操作内完成任务。
有一些细节问题:在奇偶分组后,可能要求某一行全部变。这时不需要新加一次操作,直接在每次操作的时候加上这一行的行号即可。
网格游走问题
要求你从走到,使得不碰到和的直线()。
从出发,你可以走到或者。
求方案数。
。
容斥 组合意义 翻折
如果只要求不碰到,那么这就是个经典的翻折问题。而由于本题难以不重不漏的计数,因此考虑容斥。
从走到的方案数是一个组合数。然后我们要减掉不合法的方案数。
我们想办法将每个路线赋权,使得合法的路线权值是,不合法的路线权值是。那么我们求出权值和即可得到不合法的方案数。
对于一个路线,考虑这样两个累加过程:
- 当第一次经过时减,接下来当它经过时加,接下来当它经过时又减,经过时又加一,以此类推。
- 当第一次经过时减,接下来当它经过时加,接下来当它经过时又减,以此类推。
你发现这两个过程得到的累加和的和,对于不合法的路径总是,对于合法的路径总是。
接下来我们就来算两类累加和。由于是对称的,我们只描述第一种累加和的计算过程。
考虑算所有路线的累加和的和。
- 对于第一次经过的情况,我们将关于对称得到,然后求到的方案数即可(系数是)。
- 接下来经过,这时我们将关于对称得到,然后求到的方案数即可(系数是)。
以此类推,第次翻折的系数是。
然后就做完了。
树
完全二叉树:指内部结点的儿子数都为的二叉树。
左链树:有个叶子点,且所有内部结点的右儿子都是叶子结点的完全二叉树。
定义两种操作:
- 删除某个子树;
- 对于边(是的父亲),将替换为(的其他儿子全部被删除)。
现在问有多少个个叶子结点的完全二叉树,使得无法通过若干次操作变成左链树。
。
生成函数 组合意义
这道题有两个思路方向,其中只有组合意义是可以走到最后的(目前)。
算法一
考场上想到的生成函数做法。
显然我们可以去掉所有的叶子结点。因此问题转化为求个结点,且往左走的最大次数不超过的二叉树的个数。
设表示有个内部结点,且左链(往左走的最大次数加)长度小于等于的二叉树是个数。
设。根据的DP方程容易得到
其中。
然后你算前几个就会发现分子和分母的多项式的系数有规律。
这样你可以求出分子和分母的多项式,然后做一个求逆(这题没给部分分)。
算法二
这是个组合意义的做法。为此我们直接DP。
设表示有个结点且走到当前这个点的左链(走到当前这个点,往左走的最大次数加)长度小于等于的完全二叉树是个数。按照 DFS 序DP。
有()。
容易发现这就是上文的网格游走问题。因此容斥即可。
那么答案是,因为根结点的右链末端点是DFS序最大的点。
时间复杂度。
Glow, Little Pixel, Glow
你有一个网格,沿着横竖交叉的网格线会有脉冲经过。有两类脉冲:
- 横向的脉冲一定是从左往右移动
- 纵向的脉冲一定是从上到下移动
脉冲可以记为,分别表示这个脉冲的出发时间、脉冲长度、脉冲所在的行号(列号):
- 出发时间指这个脉冲到达第列(行)的时间。
- 脉冲的移动速度是一个单位网格边长每单位时间。
- 可理解为,脉冲是个长度为单位边长的线段,即它同时覆盖了个格点。
被脉冲覆盖的格点处于激活状态。
每个格点上有一个灯泡。如果某个格点的横向和纵向在某个时刻同时被激活,那么这个点上的灯就会亮。
现在给出个脉冲,保证每一行最多一个脉冲,每一列最多一个脉冲,问最后被点亮的灯的个数。
。
建模
这题的条件比较繁琐,细节颇多,难点在于形式化的建模。
首先我们可以离散化,只考虑存在脉冲的行和列(这里的离散化是指思维过程中离散化,不一定体现在代码上)。
如果某个灯它不亮,那么要么它所在的行脉冲比列脉冲来得早,要么列脉冲比行脉冲来得早。因此我们可以对这两种情况分别统计,就可以得到不亮的灯数,进而得到点亮的灯数。
而这两种情况是对称的,只用考虑其中一种情况,然后将行列交换再做一次即可。
设表示第行的脉冲第一次到达第列的时间。假设这一行的脉冲是,那么显然。
设表示第列的脉冲恰好离开第行的时间。设这一列的脉冲是,那么有。
那么当且仅当,第行第列的灯不亮(只统计列脉冲比行脉冲来得早的情况)。
于是问题转化为求满足的格点的个数。
简单变换一下不等式得到,不等式的左边只和有关,右边只和有关。可以计数。
总时间复杂度。
Carny Magician
求字典序第小的含有个不动点的长度为的排列。不动点指满足的下标。不存在则输出。
。
贪心 溢出处理
这题是没有取模的。因此如果你的算法涉及了减法(容斥),那么就难以处理溢出的情况。
因此我们考虑不重不漏的计数。首先外壳是个贪心,将问题转化为:设表示:将个不同的数排成排列,且其中有个数无法构成不动点(可以理解为,这个数的值大于)的错排方案数。错排指没有不动点的排列。
有了这个我们就可以在贪心的过程中计算方案数了。举个例子,有个不动点的长度为的排列总数是。
然后我们写一个简单的防溢出即可:
long long add(long long x, long long y) {
return min(INF, x+y);
}
long long mul(long long x, long long y) {
if(!x || !y) return 0;
if(INF/x < y) return INF;
return x*y;
}时间复杂度。
Pivoting Points
二维平面上有个点,不存在三点共线。你可以选择一个点做为起始点,然后任意画一条只经过这个起始点的直线。
接下来以该直线过的点为轴,逆时针旋转直线,每当碰到另一个点(即两个点同时出现在该直线上)时,把轴点更换为,并且在上打个标记,然后继续旋转。
令这次旋转的价值为,旋转了后标记数量最多的点上的标记数量。
任意选择起点,求最大价值。
。
模拟
容易证明,旋转后会回到起始点。因此我们设表示以为轴,过和的直线逆时针旋转下一个碰到的点的编号。这个可以预处理。
然后模拟一下即可。每个环只会被访问一次,因此时间复杂度有保证。
不过在某些情况下一个环可能只代表的旋转,比如时就存在这样的情况。
一个简单粗暴的方法是记录一下旋转的角度,看加起来是不是约等于。
尺树寸泓
给出一棵个点的带点权的二叉树,你可以
- 把一个点左旋。
- 把一个点右旋。
- 设一个点的价值是子树点权和。求子树里结点的价值的积。
。
DFS序
这题的要点是:左旋和右旋都不会影响树的中序遍历。
而中序遍历中子树对应区间。
同时分析可得,旋转带来的修改是的。
写个树状数组维护即可。
时间复杂度。
凫趋雀跃
要求从走到,每一步可以走一个非零向量,其中,且其中有个形如的向量不能选。保证是的倍数。
问恰好走步到达的方案数。
。
容斥
本题的条件约束复杂,较为繁琐,要点是勇气。只要敢想就可以过。
如果,并且允许走零向量,那么我们发现可以把向量正交分解,即把横竖分开做,转化为一维的问题。总方案数就是两个一维问题方案数的乘积。转化后的一维问题形如:有个非负变量,要求总和为,且每个变量小于,求方案数。这可以容斥后插板。
如果不允许走零向量,那就对此套个容斥上去。
如果,那么就对此再套个容斥上去。形式化地,设表示走了次不能选的向量,走到了这个位置的方案数。然后再配合组合数就可以容斥了。
仔细算一下复杂度,发现能过。可能需要记忆化以优化。
保镖
给出一个左部个点右部个点的带点权二分图,求集合的个数,使得且存在一个匹配把中的点都覆盖,且中的点权和。
。
霍尔定理
霍尔定理指出一个二分图存在完美匹配的条件。定义表示的邻居集合。那么对于二分图,不妨设。那么存在大小为的匹配当且仅当
证明
如果存在大小为的匹配,那么此条件显然成立。
如果此条件成立,那么可以通过一个构造性的算法得到大小为的匹配:
- 初始时令匹配集合。
- 若的左部点集等于就终止算法。
- 否则找到一个左部点,然后尝试寻找増广路。
- 如果找到増广路,就増广。然后返回步骤 2。
- 否则,对于任意从出发,以左部点结束的路径,设上的左部点集合为,那么必然不满足上述条件(hall violator)。
简而言之,要点在于:如果找不到増广路,就会出现 hall violator,因此必然有増广路,因此有完美匹配。
题解
如果只选择左部点的子集,那么我们可以使用霍尔定理判断。
而如果选择了两边的点且满足题目给的条件,那么左右两边选择的点集一定分别满足霍尔定理(必要性)。
我们尝试证明:左右两边选择的点集分别满足霍尔定理的充分性。
假设左右两边分别满足霍尔定理。
那么我们先给左边的点集找一个完美匹配。
然后依次考虑右边点集里的点:
- 如果这个点已经被覆盖,就不管它。
- 否则我们就増广。由于右边满足霍尔定理且右边的点集没满,因此一定有増广路。而且増广的过程只会覆盖更多的点。
这样就证明了充分性。
Two Buildings
给出长度为的序列,求。
。
分治 决策单调性
考虑分治。那么我们在左边选一个,右边选一个。不妨令,将问题转化为:左边选一个,右边选一个,求的最大值——即二维平面上的矩形面积。
这个问题目前看不到什么性质。不过由于是最优化问题,因此我们考虑添加一些限制来导出我们需要的性质。
如果存在使得,,那么就是无用的。于是我们可以把右边的点筛选一下,剩下的点满足横坐标单增的同时纵坐标递减。
左边同理,也可以这么筛一下。
这时就出现了可供利用的性质:决策单调性。
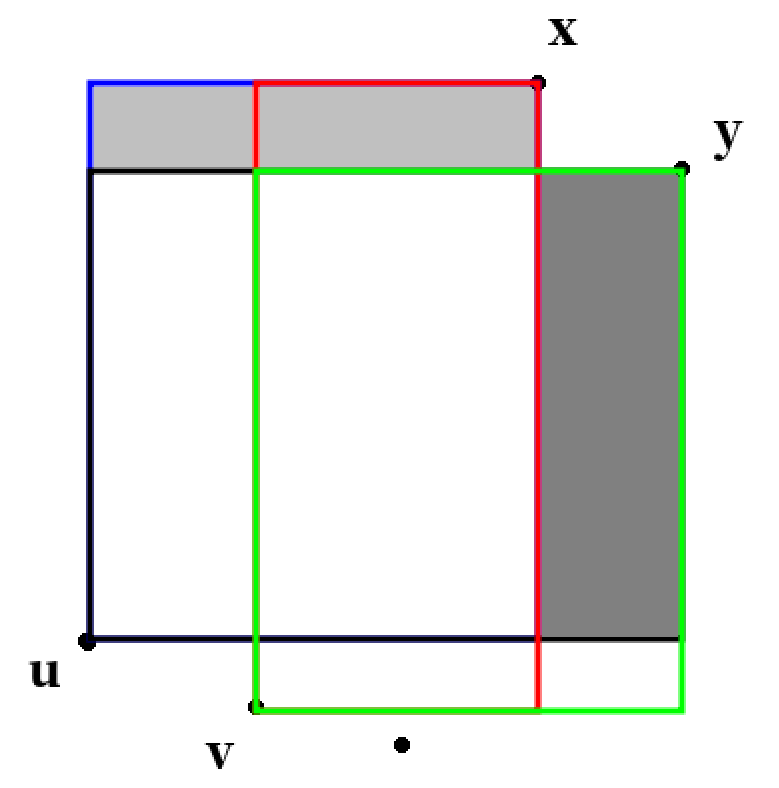
如图。假设对应的最优决策是。那么设浅灰色面积为,深灰色面积为,则有。
因此对于右边的来说,如果选择左边的,那么显然是劣于选择的。
这就证明了决策单调性。然后就可以再分治了。
时间复杂度。
修订记录
- 2021年3月21日 第6次修订
- 2021年3月17日 第5次修订
- 2021年3月13日 第4次修订
- 2021年3月12日 第3次修订
- 2021年3月11日 第2次修订
- 2021年3月10日 创建文章