多项式进阶
文章目录
洛必达法则
若函数和满足以下条件:
- ;
- 在的某空邻域内两者均可导,且;
- ,其中可为非正常极限。
则
通俗地说,如果在处的极限都是,那么在处的极限可以通过他们的导数来求。
多项式除法
给出多项式,求出,满足,且。注意这里不是模意义下。表示多项式最高次项的次数。
定义一个变换
该变换的实质是把多项式的系数翻转过来了。代入得到
由于,那么不妨设。稍作变换得到
那么容易发现,在模意义下,就没了:
这样我们可以求出。
由于,因此。于是
这样使用多项式求逆即可得到,反代回去可求出。
时间复杂度。
多点求值
给出,求,其中与同阶。
考虑分治。设,。
容易发现。那么构造。显然有满足。因此左边递归下去求值。右边同理。
时间复杂度。在实现的过程中需要预先把所有的函数都存下来,因此空间复杂度是。
快速插值
给出。那么我们可以唯一确定一个次多项式。求出这个多项式。
用拉格朗日插值可以得到
分上下两部分处理。
第一部分
考虑对于每个求出。
设。那么可以分治 NTT 计算出来,时间复杂度。
容易发现。但是如果我们直接做次多项式求逆的话复杂度就不对了。
利用洛必达法则,设。因为,且两个函数都在邻域内可导,因此得到
那么对求出在处的点值即可。这样就求出了所有。时间复杂度。
第二部分
求出后,原式可以表示为
同样考虑分治,设
那么如果我们求出了这 4 个多项式,那么可以得到。两边递归求解即可。
时间复杂度,空间复杂度,因为多点求值带一个的空间复杂度。而第二部分的计算是可以把空间减小到的,不过直接动态开空间也只增大了空间常数,没有改变空间复杂度。
多项式复合逆
对于两个多项式函数,如果,称互为复合逆。
容易证明。但是多项式复合逆没有时间复杂度的做法。但可以使用拉格朗日反演在的时间内计算出某一项。
拉格朗日反演
对于两个多项式函数,如果,那么
还有一个扩展形式:
其中是另一个多项式函数。
大朋友与多叉树
题意:求有多少棵有根树,满足有个叶子结点,内部结点的儿子数都属于集合,且。注意,儿子之间是有顺序的。
例如当时:
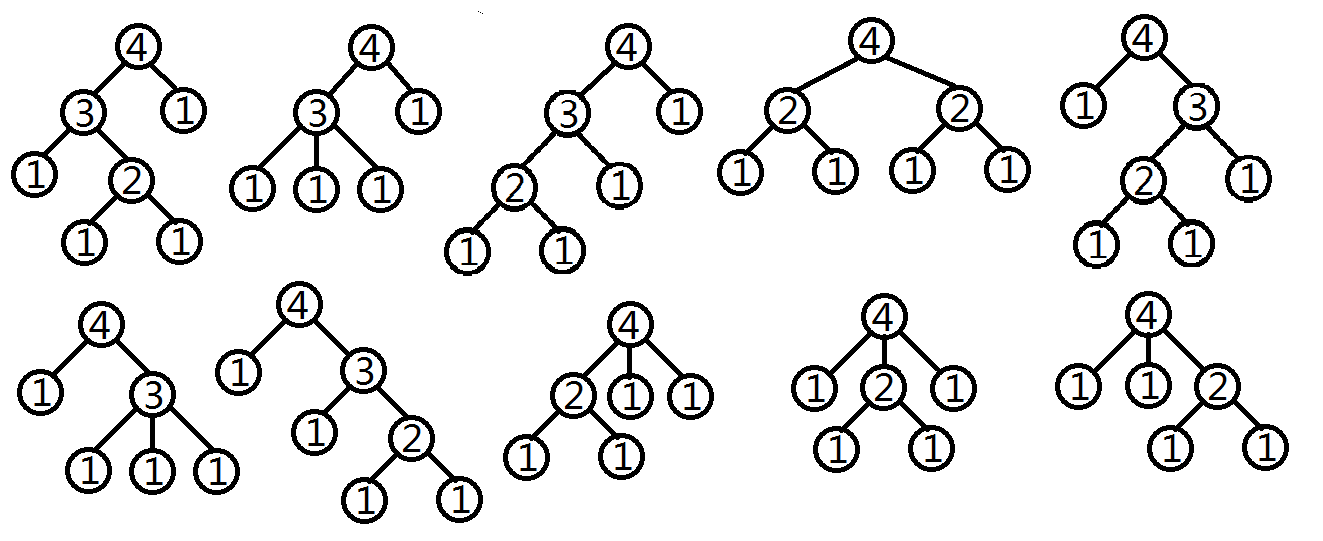
定义两个普通生成函数
其中是的答案。考虑根结点的孩子数为,此时方案数的生成函数显然为。从这个思路出发,可以得到
加上一个是考虑的情况。可以得到,因此与互为复合逆。
使用拉格朗日反演得到
在模意义下直接求值即可。一个技巧是把后面的式子转化为的形式,这样常数项为 1,可以多项式来求幂。
时间复杂度。
仙人掌计数
仙人掌:如果一个简单无向连通图的任意一条边最多属于一个简单环,我们就称之为仙人掌。所谓简单环即不经过重复的结点的环。
求个点带标号的仙人掌数量。
考虑有根仙人掌的指数生成函数为。那么求出来后把方案数除以就是答案。我们可以将仙人掌的构成分成两种部分:
- 从根结点连出去的独立边,相当于接一个仙人掌出去。一条边连出去的生成函数是,多条边之间不区分顺序,因此方案数是。
- 包含根结点的一个简单环,环上除了根结点之外的每个结点都挂一个仙人掌。由于我们要考虑环上结点之间的顺序,因此假设环长为,那么个仙人掌按序排列的生成函数是。考虑到是一个环,因此每个排列被正着反着各算了一次,因此长度为的环的生成函数是。那么一个环的生成函数就是。多个环之间是不区分顺序的,因此多个环的方案数是。
综上,环和独立边互不相关,总方案数是,再加上根结点本身得到
稍作整理得到
考虑牛顿迭代法。
方法一
设
那么显然我们要求。应用牛顿迭代得到
对求导得到
如何理解式子中的?我们把它理解为与不相关的一个常量即可。常量的导数是。
最后得到
方法二
方才的式子可以变换为
因此设
同样的方法,对求导得到
因此可以得到
两种迭代方式是等价的。由于是 EGF 最后别忘了乘上。
点双连通图计数
如果一个无向连通图删去任意一个点都仍然是连通的,我们就称为点双连通图。
求个点带标号点双连通图的个数。
同样地,设表示个点的点双连通图的 EGF。设表示个点有根连通图的 EGF。
设表示带标号无向图数的生成函数,那么得到。
我们考虑用表示。考虑有根无向图的包含根结点的点双连通分量。假设大小为,那么除了根结点之外的点都可以挂一个有根连通图,因此方案数是。对于个不区分顺序的有根连通图的根结点,再加上根结点,因此一个点双连通分量的方案数是。多个点双连通分量之间不区分顺序,因此总方案数是。再加上根结点本身得到
然而这个方程无法牛顿迭代。设的复合逆是,那么得到
据说使用扩展拉格朗日反演可以解决。
修订记录
- 2020年5月28日 创建文章