AI 系统速通笔记之数据预处理

本文的标题非常不负责任，概 AI 基础这门课本身的课程内容极具争议的缘故。

拿到了数据后要先进行一些预处理才会拿去做模型训练。这里面的门道比想象中多。

$$\gdef\vx{\mathbf{x}}$$

概述

首先我们理清数据预处理的流程，用到的比较具体的技术和方法会在下面专门讲。

首先，我们需要清除一些错误的数据。一个比较有效的统计方法是使用箱线图来去除极端的值。

有些数据的特征可能含有缺失项，如果确实不具备参考价值可以直接删除（pandas 中可以调用 dropna）。但是如果要利用含有缺失项的特征，我们需要适当给予补充修复。常见的做法是使用已有数据平均值/中位数/默认值/相邻的值补全，或者采用某种公式插值（线性插值，例如按照时间排序的温度信息）。

接下来我们需要做一些数据转化。对于实数特征我们可以按照某种公式进行规范化，对于图片我们可以裁剪、压缩等等，对于文本数据可以做分词和词的分类（英文单词的不同变形）等等。

在这之后，我们可以使用特征工程的一些方法来筛选、简化、合并特征，使得之后的（深度）学习过程更加容易。为此我们主要进行特征选择，很多特征选择的方法也会对应特征的合并或者训练上的调整。

箱线图¹

箱线图主要用于检测数据中的离群值。

设$Q_2$表示所有数值的中位数，$Q_1$表示小于$Q_2$这部分值的中位数（第一四分位数），$Q_3$为大于$Q_2$这部分值的四分位数（第二四分位数）。$[Q_1, Q_3]$就是箱子的范围。

称$Q_3 - Q_1 = \mathrm{IQR}$为四分位间距 Interquartile range。则$[Q_1 - 1.5\mathrm{IQR}, Q_3 + 1.5\mathrm{IQR}]$就是线段的范围。

落在线段之外的值就是离群值（outlier）。下面就是本次作业的房子数据各个特征的箱线图，可以发现确实有许多离群值：

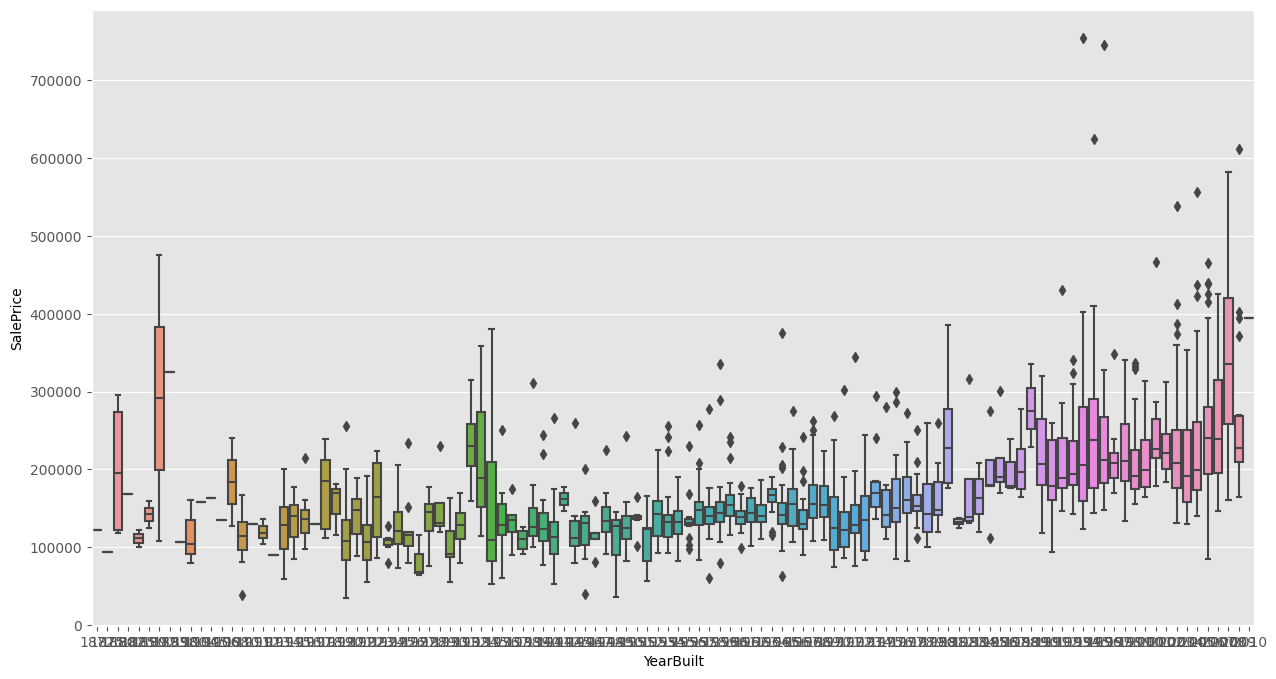
用到的库是 python 的 seaborn。

信息熵

首先我们给出信息熵的定义：对于随机变量$X$，和其服从的概率分布$p$，定义

$$H(X) = -\sum_{x} p(x)\log p(x)$$

信息熵可以理解为系统内不同事件信息量的期望。

对于两个随机变量$X, Y$和其联合分布，我们可以定义联合熵：

$$H(X, Y) = -\sum_{x, y} p(x, y)\log p(x, y)$$

它描述一个联合分布$p(x, y)$的不确定程度。此外，已知$X$时$Y$的不确定程度可以用条件熵表征：

$$\begin{align} H(Y | X) &= \sum_{x} p(x) H(Y | X = x) \\ &= -\sum_{x} p(x) \sum_y p(y | x) \log p(y | x) \\ &= -\sum_{x, y} p(x, y) \log p(y | x) \\ \end{align}$$

条件熵与联合熵的关系是$H(X, Y) = H(Y) + H(X | Y) = H(X) + H(Y | X) = H(Y, X)$，可以通过推导证明。有了熵，我们就可以定义互信息

$$I(X, Y) = H(X) + H(Y) - H(X, Y)$$

结合一下条件熵与联合熵的关系，可以发现$I(X, Y) = H(X) - H(X | Y) = H(Y) - H(Y | X)$，可以画出直观易懂的维恩图。

决策树

决策树可以将一组数据按照其特征进行分类，其中

• 根节点包含所有数据
• 每个非叶子节点中的数据会按照某个属性进行分类，将分类的数据放在子节点中
• 每个叶子节点对应决策结果

要构建决策树，主要考虑的问题是选择什么属性来划分数据最优。直观上我们希望划分后尽量是“均分”的，而不是所有数据归为一类。为了衡量划分的优秀性，我们可以结合上文提到的信息熵。

划分准则

我们可以使用信息增益来度量划分的优秀性。为此首先我们要度量数据集$D$在分类标签集$K$下的纯度：

$$H_K(D) = -\sum_{k \in K} \frac{|D_k|}{|D|} \log \frac{|D_k|}{|D|}$$

其中$D_k$表示标签为$k$的数据集合，$\frac{|D_k|}{|D|}$自然表示划分到$k$类别所占的比例。$H(D)$越高意味着样本纯度越低。

特征$A$对$D$的信息增益定义为

$$g(D, A) = H_K(D) - \sum_a \frac{|D^{A=a}|}{|D|} H_K(D^{A=a})$$

单从实现的角度，$H_K(D)$可以不管。后面的和式描述的是特征$A$的每个取值下样本的纯度。显然纯度越有利于分类，因此我们取一个负号在前面。

信息增益还可以理解为属性与标签之间的互信息。

但是信息增益的问题是如果$A$的取值过多，每个取值下的数据过少，这样的分类效率和泛化性都不高。

我们还可以采用增益率作为划分准则：

$$g_R(D, A) = \frac{g(D, A)}{H_A(D)}$$

这样就缓解了上述问题。

另一种划分准则是基尼指数（Gini index，也称 Gini Impurity）：

$$\mathrm{Gini}(D) =\sum_{k \in K} \frac{|D_k|}{|D|}\left(1- \frac{|D_k|}{|D|}\right) = 1 - \sum_{k\in K} \left( \frac{|D_k|}{|D|} \right)^2$$

特征$A$对$D$的 Gini 指数为

$$\mathrm{Gini}(D, A) = \sum_{a \in A} \frac{|D^{A = a}|}{|D|}\mathrm{Gini}(D^{A=a})$$

$\mathrm{Gini}(D, A)$越小，意味着以特征$A$划分后信息量越少，说明这种划分对提升数据纯度的帮助越大。

事实上我们可以类比信息增益定义 Gini Decrease 为$\mathrm{Gini}(D) - \mathrm{Gini}(D, A)$。

回归树

上面描述的都是利用离散的特征对数据分类的问题。

如果特征是连续的值，我们可以将其按照某种分度离散化。

如果目标是对数据的标签做回归分析（例如房价预测），我们只需要稍微魔改一下决策树就能解决这个问题。为此我们引入回归树。

回归树与决策树结构相同，但是对于集合纯度我们使用$L_2$估计。设$L(D)$表示数据集的方差，$L(D, A) = \sum_a L(D^{A = a})$，那么最优特征定义为

$$A^{\ast} = \arg\min_{A} L(D, A)$$

决策树和回归树在 sklearn.tree 中均有对应的 API 可以调用。

数值规范化

常见的规范函数有

• 线性映射为$[a, b]$之间的值（min-max normalization）：

  $$x_i' = \frac{x_i - \min}{\max - \min}(b - a) + a$$

• 映射成均值为$0$，方差为$1$的数据分布（z-score normalization）：

  $$x_i' = \frac{x_i - \bar{x}}{\mathrm{std}(x)}$$

• 十进制缩放（decimal scaling）：

  $$x_i' = \frac{x_i}{10^j}$$

  其中$j$为使得$\max_i |x_i'| < 1$的最小的$j$。

• 对数缩放（log scaling）：

  $$x_i' = \log x_i$$

特征选择

特征选择解决问题是：当可用的特征过多时，选择其中最合适的作为子集，最大化训练模型的效率。首先我们可以使用 Pearson 相关系数、互信息、Gini index 等方法来判断两个特征的相关程度。我们也可以将特征选择的过程和模型训练结合到一起，也就是嵌入法。还可以将特征选择看成搜索问题。

Pearson 相关系数

中学知识：

$$r = \frac{\sum(x - \bar x) (y - \bar y)}{\mathrm{std}(x)\mathrm{std}(y)}$$

在 scipy 中有对应的 API。

嵌入法

对于一个回归问题，以线性回归为例，特征可以抽象为$d$维向量$\vx$，回归目标为$y$。对于多个数据$(\vx_1, y_1), \ldots, (\vx_n, y_n)$，目标函数是$\min\sum(y_i - \hat{y}_i)^2$。使用的模型是$\hat{y}_i =\mathbf{w}^T\vx_i$。

而 Lasso 方法则在线性回归的基础上对$\mathbf{w}$的值进行$L_1$正则化：

$$\min \sum (y_i -\hat{y_i})^2 + \theta \sum_{k = 1}^n |w_i|$$

在$L_1$正则化下，大部分系数会是一个接近$0$的数字，剩下的绝对值很大的系数对应的是重要的特征。这种方法统称嵌入法。

值得一提的是，Ridge² 回归也使用了相似的思想，即在最小化损失的同时对参数进行规范化，如果要用它做特征选择可能会需要做一些矩阵运算。

迭代法

如果将特征选择看成搜索问题，暴力搜索有$2^N$种情况，十分不优秀。

此时我们可以使用贪心的方法，从空集开始每次加入一个特征，并计算模型的性能提升程度（递增）；或者从全集开始每次减少一个特征，并计算模型的性能降低程度（递减）。

Gini Importance³

也称 Mean Decrease in Impurity (MDI)。Gini Importance 的实现方式目前存在争议。这里我们讲的是 sklearn 的实现方法⁴⁵。

设决策树的结点集合为$T$，$D_u$表示结点$u$上的数据，$A_u$表示$u$上用于分割的特征。那么特征$A$的 Gini Importance 定义为

$$\sum_{u}[A_u = A] [\mathrm{Gini}(D_u) - \mathrm{Gini}(D_u, A_u)]\frac{|D_u|}{|D|}$$

Permutation Importance

也称 Mean Decrease in Accuracy (MDA)。

我们可以将数据的某个特征打乱顺序，计算打乱前和打乱后的准确性$a_0, a_1$，那么这个特征的重排重要性就是$\frac{a_0 - a_1}{a_0}$，以此来估计哪些特征具有保留价值。

在 sklearn.inspection 中有对应的 API。

SHAP⁶

SHAP 是一个用于特征解释的工具，也可以用于特征选择。

相关连接

¹. https://en.wikipedia.org/wiki/Box_plot ↩

². https://en.wikipedia.org/wiki/Ridge_regression ↩

³. https://medium.com/the-artificial-impostor/feature-importance-measures-for-tree-models-part-i-47f187c1a2c3 ↩

⁴. https://scikit-learn.org/stable/modules/tree.html#tree-mathematical-formulation ↩

⁵. https://github.com/scikit-learn/scikit-learn/blob/108486011b833cef8061615d926e2883941b9123/sklearn/tree/_tree.pyx#L1114 ↩

⁶. https://github.com/slundberg/shap ↩